|
Exercise 1.
a) If you multiply two non-repeating decimals, can you
ever get a repeating decimal?
b) If you multiply two repeating decimals, can you ever
get a non-repeating decimal?
Exercise 2.
a) If
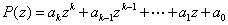 is a polynomial, show that
is a polynomial, show that
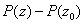 is divisible by
is divisible by
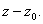
b) Deduce that
 is divisible by
is divisible by
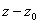 if
if
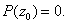
c) Deduce that if
 is a polynomial of degree
is a polynomial of degree
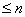 and
and
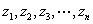 are
are
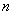 distinct zeros of
distinct zeros of
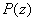 ,
then there is a constant ,
then there is a constant
 such that
such that

d) If
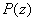 has degree
has degree
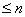 and vanishes at
and vanishes at
 distinct values
distinct values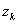 ,
show that ,
show that
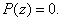
e) If
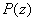 and
and
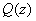 are polynomials of degree
are polynomials of degree
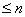 which agree for
which agree for
 distinct values
distinct values
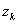 ,
show that ,
show that
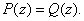
Exercise 3.
If, for each real number
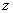 ,
the polynomials ,
the polynomials
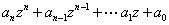 and
and
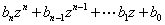 agree on some neighborhood of
agree on some neighborhood of
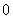 ,
show that they must agree for all complex numbers ,
show that they must agree for all complex numbers
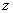 . .
Exercise 4.
Find the sum and product of the zeros of a polynomial in
terms of the coefficients, and then apply to the equation
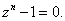
Exercise 5.
If
 are the zeros of a polynomial
are the zeros of a polynomial
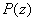 of degree
of degree
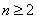 and
and
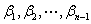 are the zeros of a polynomial
are the zeros of a polynomial
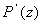 ,
show that ,
show that
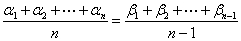
Exercise 6.
Suppose
 is an entire function with
is an entire function with
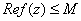 for some positive number
for some positive number
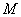 .
Show that .
Show that
 is constant.
is constant.
Exercise 7.
Suppose
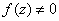 is an entire function with
is an entire function with
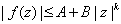 for some positive numbers
for some positive numbers
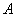 and
and
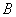 and some non-negative integer
and some non-negative integer
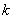 .
Show that .
Show that
 is a polynomial of degree at most
is a polynomial of degree at most
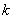 . .
Exercise 8.
A real-valued function
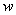 which is continuous in a region
which is continuous in a region
 and satisfying
and satisfying
 there is called a subharmonic
function. Show that
there is called a subharmonic
function. Show that
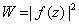 is a subharmonic function on any region where
is a subharmonic function on any region where
 is analytic.
is analytic.
Exercise 9.
Suppose
 is an entire function such that Re
is an entire function such that Re
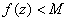 for some constant
for some constant
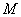 and all values
and all values
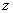 .
Show that .
Show that
 is a constant function
is a constant function
Exercise 10.
Let
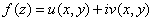 be a holomorphic function in a domain
be a holomorphic function in a domain
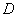 .
If .
If
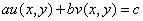 in
in
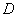 (
(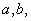 and and
 being real constants not all zero), then
being real constants not all zero), then
 is constant in
is constant in
 |

